Lambang, Makna, Penjelasan Makna dan Contoh penggunaan lambang matematika:
Menyatakan kesamaan (makna atau nilai) antara pernyataan di sebelah kiri lambang dengan pernyataan disebelah kanan lambang.
Menyatakan bahwa ungkapan di sebelah kanan lambang merupakan definisi dari ungkapan di sebelah kiri lambang.
Contoh:  , menyatakan ungkapan "momentum linier P didefinisikan sebagai perkalian massa m dengan kecepatan partikel v"
, menyatakan ungkapan "momentum linier P didefinisikan sebagai perkalian massa m dengan kecepatan partikel v"
"diungkapkan dalam bentuk" atau "diwakili oleh"
Menyatakan bahwa ungkapan di sebelah kanan lambang merupakan salah satu bentuk tampilan dari ungkapan di sebelah kiri lambang.
Contoh: , menyatakan "
, menyatakan " merupakan salah satu bentuk tampilan operator
merupakan salah satu bentuk tampilan operator  (yaitu di ruang posisi dalam sistem cartesian)"
(yaitu di ruang posisi dalam sistem cartesian)"
"nilainya sekitar" atau "dapat didekati sebagai"
Menyatakan bahwa ungkapan disebelah kanan lambang merupakan nilai penghampiran (pendekatan) dari besaran yang ditulis di sebelah kiri lambang.
Contoh: Untuk x sangat besar maka .
.
"konjugate kompleks"
Menyatakan konjugate kompleks bagi fungsi (bilangan) yang ditulis sebelum tanda *.
Contoh: Jika maka
maka  .
.
(dua fungsi yang dipisahkan dengan tanda koma dan ditempatkan di dalam kurung biasa)
"perkalian skalar"
Menyatakan perkalian skalar antara fungsi yang ditulis di sebelah kiri tanda koma dengan fungsi yang ditulis di sebelah kanan tanda koma.
Contoh:,g(x)&space;\right&space;)\equiv&space;\int&space;f^{*}(x)g(x)dx) .
.
(huruf besar bertopi)
"operator"
(dua operator yang dipisahkan dengan tanda koma dan ditempatkan di dalam tanda kurung siku)
"komutator"
Menyatakan komutator yang dibentuk oleh operator yang ditulis di kiri tanda koma dengan operator yang di tulis di kanan tanda koma.
Contoh:![\left [ \hat{A},\hat{B} \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;\hat{A},\hat{B}&space;\right&space;]) , komutator yang dibentuk oleh operator
, komutator yang dibentuk oleh operator 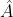 dan
dan  .
.
(fungsi atau vektor yang ditempatkan dalam tanda garis tegak di kiri dan kanan)
"nilai mutlak" atau "absolut"
Contoh: : modulus ata nilai vektor a.
: modulus ata nilai vektor a. &space;\right&space;|) : nilai mutlak bagi
: nilai mutlak bagi ) .
.
LAMBANG VEKTOR DAN SKALAR
 , a dan b menyatakan vektor, sedangkan a dan b menyatakan skalar.
, a dan b menyatakan vektor, sedangkan a dan b menyatakan skalar.
Baca Juga: Penurunan Rumus Energi Gas Monoatomik
"diungkapkan dalam bentuk" atau "diwakili oleh"
Menyatakan bahwa ungkapan di sebelah kanan lambang merupakan salah satu bentuk tampilan dari ungkapan di sebelah kiri lambang.
Contoh:
"nilainya sekitar" atau "dapat didekati sebagai"
Menyatakan bahwa ungkapan disebelah kanan lambang merupakan nilai penghampiran (pendekatan) dari besaran yang ditulis di sebelah kiri lambang.
Contoh: Untuk x sangat besar maka
"konjugate kompleks"
Menyatakan konjugate kompleks bagi fungsi (bilangan) yang ditulis sebelum tanda *.
Contoh: Jika
(dua fungsi yang dipisahkan dengan tanda koma dan ditempatkan di dalam kurung biasa)
"perkalian skalar"
Menyatakan perkalian skalar antara fungsi yang ditulis di sebelah kiri tanda koma dengan fungsi yang ditulis di sebelah kanan tanda koma.
Contoh:
(huruf besar bertopi)
"operator"
(dua operator yang dipisahkan dengan tanda koma dan ditempatkan di dalam tanda kurung siku)
"komutator"
Menyatakan komutator yang dibentuk oleh operator yang ditulis di kiri tanda koma dengan operator yang di tulis di kanan tanda koma.
Contoh:
(fungsi atau vektor yang ditempatkan dalam tanda garis tegak di kiri dan kanan)
"nilai mutlak" atau "absolut"
Contoh:
LAMBANG VEKTOR DAN SKALAR
- Vektor dilambangkan dengan huruf latin yang ditulis tegak dan tebal. Contoh: p, F, i.
- Skalar dilambangkan dengan huruf latin yangdicetak miring, tidak tebal. Contoh: p, F.
Baca Juga: Penurunan Rumus Energi Gas Monoatomik












